最高のコレクション 扇形 弧の長さ 公式 110097-扇形 面積 公式 弧の長さ
円の周りの長さ(円周) ①直径×314=円周 r ×2×S=2Sr 扇形の弧の長さと面積 360 x =弧の長さ ℓ=2Sr × 360 x 半径×半径×314× 360 x =面積 S =Sr 2× 360 x 横 縦 〔 a〕 横〔b 〕 一辺〔a〕 〕 一もしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2 扇形の面積の公式:円弧×半径/2 に代入 もしくは、円全体の面積 πr 2 に割合 θ/2π を掛ければ求「弧の長さ」や「面積」は、円の公式から求めることができるんだ。おうぎ形は、 円を分割 したものだから、 円の公式 に 360°のうちのどれくらいの角度を切り取ったか をかけてやればいいんだね。

これの表面積の求め方の解説をお願いしたいです W Clear
扇形 面積 公式 弧の長さ
扇形 面積 公式 弧の長さ-國小_數學_1121圓與扇形的周長 講師林雨嫻 講師簡介 林雨嫻老師,目前任教於溪口國小。喜歡與孩子一起學習,熱愛教育。 課程介紹 圓周長公式的演進。利用圓周長來求弧長。並且認識利用圓心角來求弧長。主要的公式有:圓周長=直徑x314。扇形弧長公式扇形圓周長公式精采文章扇形圓周長公式,橢圓形圓周長公式,正方形周長公式,周長計算公式網路當紅,長方形面積公式,扇形面積公式 1/2(r)^2Θ 弧長公式 r Θ (Θ為角度) 參考資料: 我自已 1 001 意見者: MrNatural ( 初學者 2 級 ) 發表時間: 0145 檢舉 ~老人家 ,弧長公式n是




扇形の弧の長さの求め方 公式と計算例
扇形 ~弧の長さ、半径から中心角を求める~ 作者 Enpitsu さん 実行数 扇形 ~弧の長さ、半径から中心角を求める~ 作者はじめに ここでは、扇の弧の長さとその面積の求め方・公式について説明します。 扇の弧の長さ この図形は、半径が「r」、中心角が「α」、弧の長さが「l」の扇です。このとき扇の弧の長さ「l」は次の公式で求めることができます。 なんで 扇形が完全な円(中心角360°)に対してどれくらいの割合の大きさになっているのかを、中心角 a を用いて a 360 で表しています。 完全な円の場合円周は 2πr なので、弧の長さはこれに a 360 をかけた値になります。 『直径 × 314 × 中 心 角 360』⇒『2πr × a 360』 ちなみに、扇形の弧の長さについても考え方は詳しく解説しています。 おうぎ形の弧の長さと面積の求め
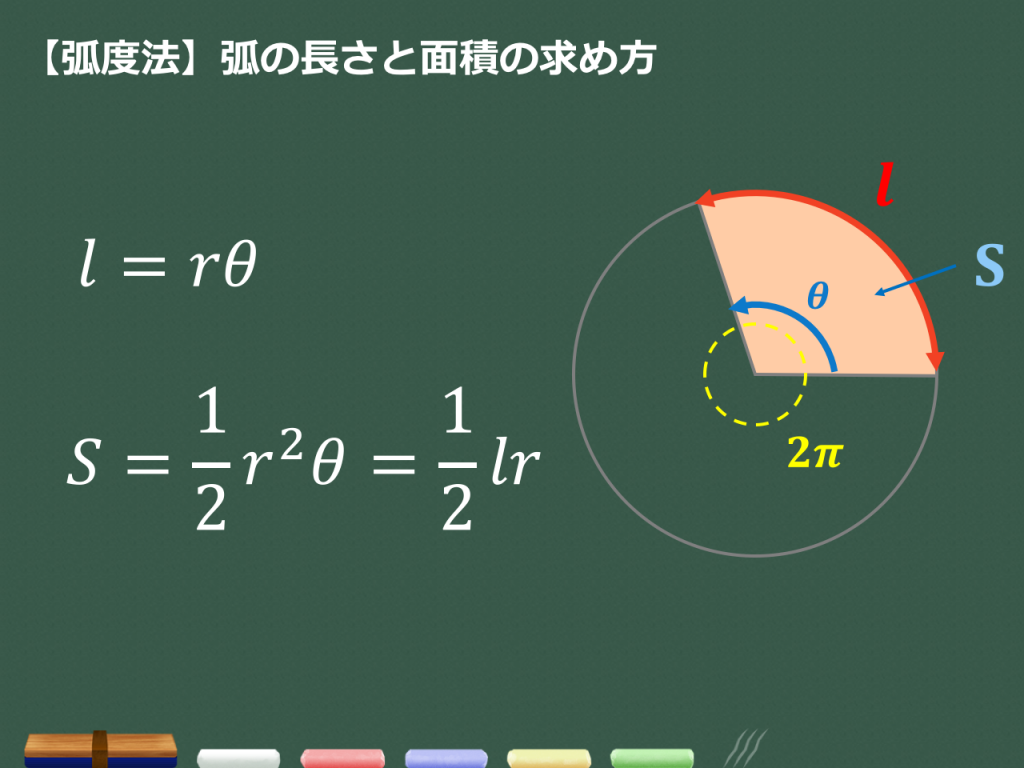
"扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明扇形的弧長與面積公式: 若圓半徑為 r,扇形 COD 的圓心角 ∠COD=θ(弧度),2π, ≤ θ 0 ≤ 如下圖所示,令扇形的弧長為 s,面積為 A,則: 弧长公式 l = n(圆心角)× π(圆周率)× r(半径)/180=α (圆心角弧度数)× r(半径) 在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πr,所以n°圆心角所对的弧长为l=n°πr÷180°(l=n°x2πr/360°) 例:半径为1cm,45°的圆心角所对的弧长为 l=nπr/180
弧の長さと面積の公式 <証明> 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さをl、面積をSとするとき ※θは、度数法ではなく弧度法



3分でわかる 弧度法 ラジアン の要点 度数法との変換 合格サプリ




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
(弧の長さ)=(半径)×(円周率)×(中心角)÷180 なので、半径は 半径=(弧の長さ)÷(円周率)÷(中心角)×180です。 扇形の半径の求め方教えてください! なんか、公式みたいなやつNo003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m 扇形の弧の長さの公式弧度法 半径が \(r\)、中心角が \(\theta\) \((\mathrm{rad})\) の扇形の弧の長さ \(l\) は \begin{align} \color{red}{l = 2\pi r \cdot \frac{\theta}{2\pi} = r



扇形と円 中学から数学だいすき




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
半圓周長公式圓周長公式精采文章圓周長公式,橢圓形圓周長公式,扇形弧長公式,長方形面積公式網路當紅,求圓周長公式,圓周長=直徑 ×314 半圓周長=(圓周長 ÷ 2)+直徑 括號裡的要先算喔!!~~~希望你選我~~~ 參考資料 Me 相關詞: 周長公式, 圓的周長, 扇形周長, 橢圓周長, 三角形周扇形の弧の長さの公式と求め方 扇形の弧の長さの公式は下記です。 l=rθ ※lは弧の長さ、rは扇形の半径、θは角度(ラジアン) 半径5、角度が36°の扇形があります。扇形の弧の長さを求めてください。 ポイントは角度36°をラジアンに変換することです。C 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (3)三角函數




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
弯曲的AB部分为弧arc OE为边心距 三角形AOB为三角区 ED 是拱高 弧长计算公式为: (Central Angle / 180°) •π • r 黄色区域为扇形 扇形面积公式为: (Angle AOB / 360°) •π • r² 绿色面积为拱高面积 此面积大小=扇形面积- AOB三角形扇形の弧の長さ( l ength) 公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心角}}{360^\circ} $の割合をかけることで求められます。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があったとしよう。




これの表面積の求め方の解説をお願いしたいです W Clear



1
弧の長さ L = r θL=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。 ※180°以上の中心角の場合、および2つ解がある場合にも対応しました。 2分でわかる!扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね?? それじゃあ、 扇形の弧の長さの公式 をみていこう! 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




数学 弧度法と扇形 さくらの個別指導 さくら教育研究所 Skredu
扇形の公式はこう変わる 弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, と導け, 扇形の面積 は, 度数法の公式 をradに置き換えて, また, 扇形の弧の長さの公式より 扇形の公式にあてはめると s = 3×3×π×90/360 = 9π/4 となります。 扇形の公式は覚える必要がない おうぎ形の公式は、ぱっとみるとちょっと長いと思いませんか? 実はこの公式、なぜこの式になるのかさえわかっていれば、覚える必要はありません。Boris的分享小站 186萬 位訂閱者 訂閱 圓的周長與面積 (16)扇形弧長計算的練習 複製連結 資訊 購物 取消靜音 如果經過一段時間仍未開始播放,請試著重新啟動您的裝置。




扇形の弧の長さの求め方 公式と計算例




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。弧长公式 弧长公式是平面几何的基本公式之一。 弧长公式 叙述了弧长,即在圆上过两点的一段弧的长度,与半径和圆心角的关系。 公式为l=πrα/180弧度法における弧の長さの公式 半径 r r r ,中心角 θ \theta θ ラジアンの扇型の弧の長さは r θ r\theta r θ 例えば,半径が 2 2 2 で中心角が π 4 \dfrac{\pi}{4} 4 π ラジアンである扇形の弧の長さは, 2 × π 4 = π 2 2\times\dfrac{\pi}{4}=\dfrac{\pi}{2} 2 × 4 π = 2 π と計算でき




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r,跟角度要我們求扇形的弧長或面積,我們就可以輕鬆的套公式把它算出來了弓形 (緑)は、割線/弦 (破線)と弧 (緑の領域の天井)で囲まれる 扇形の高さ=半径 R は、弦からの高さ h と深さ d の和 円の 半径 を R, 中心角は θ rad = α ° とし、弦の 長さ c および 弧長 s と 矢 の長さ h および扇形の三角形部分の高さを d とする。 円の 扇形のまわりの長さは、 扇形の弧の長さ+半径×2 で求められます。 この扇形の弧の長さ=18×314× 1 ° 360 ° =14(cm) よって、求める扇形のまわりの長さは 14+9×2=3684(cm) 答え 3684㎝ ~平面図形の面積・まわりの長さを求める公式まとめ
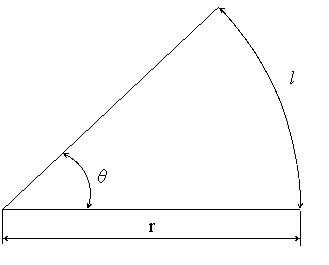



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の面積の求め方 公式と計算例




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
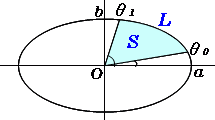



楕円扇形の面積 高精度計算サイト
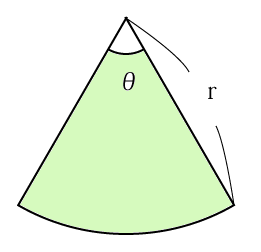



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
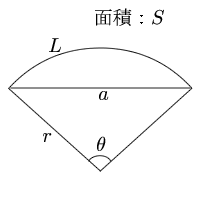



扇形 面積の計算 計算サイト




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
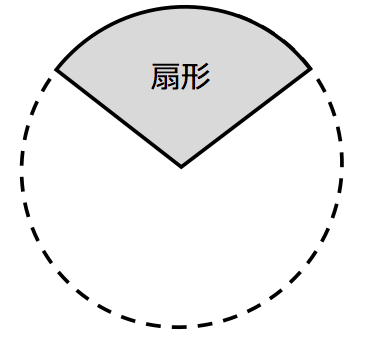



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




扇形の中心角の求め方を教えてください Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく



1



1



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




弓形の面積 香料ゐっすゐの夢




数ii 三角関数弧度法 弧の長さ 扇形の面積 Youtube




扇形の面積 ぜひ 弧の長さ を使ってみて 15 Do Your Best Haruka Saki
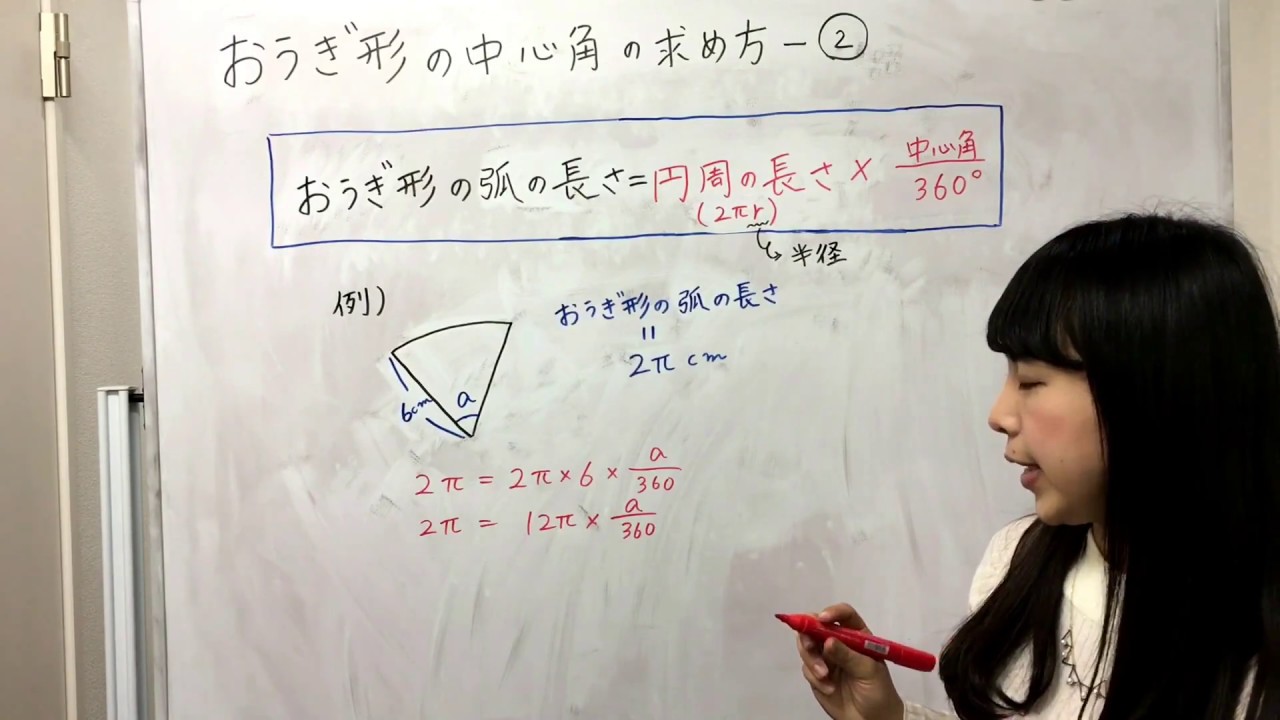



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube



扇形の公式 面積 弧の長さ 弦の長さ 数学 エクセルマニア




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




扇 おうぎ 形の面積を求める公式と弧の長さの求め方
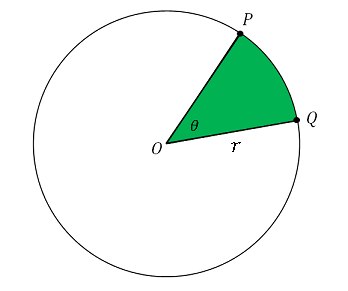



扇形の弧の長さと面積




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円弧面積の計算式




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち
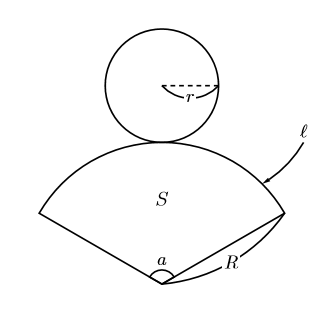



中学数学 円錐関連の公式の導出 数樂管理人のブログ




扇形の弧の長さの求め方 公式と計算例



3




数学というより算数です 円錐の側面積について Okwave




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強



扇形の弧の長さと面積 時習館 ゼミナール 高等部
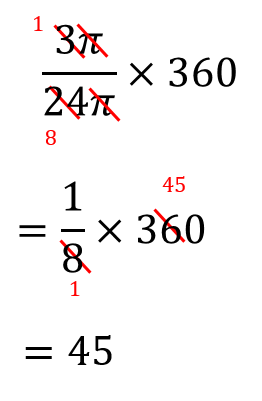



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




弧度を利用した扇の弧の長さと面積の求め方 数学ii By Okボーイ マナペディア
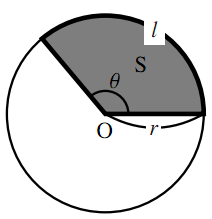



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear




円 扇形 の面積 周や弧の長さの公式 数学fun
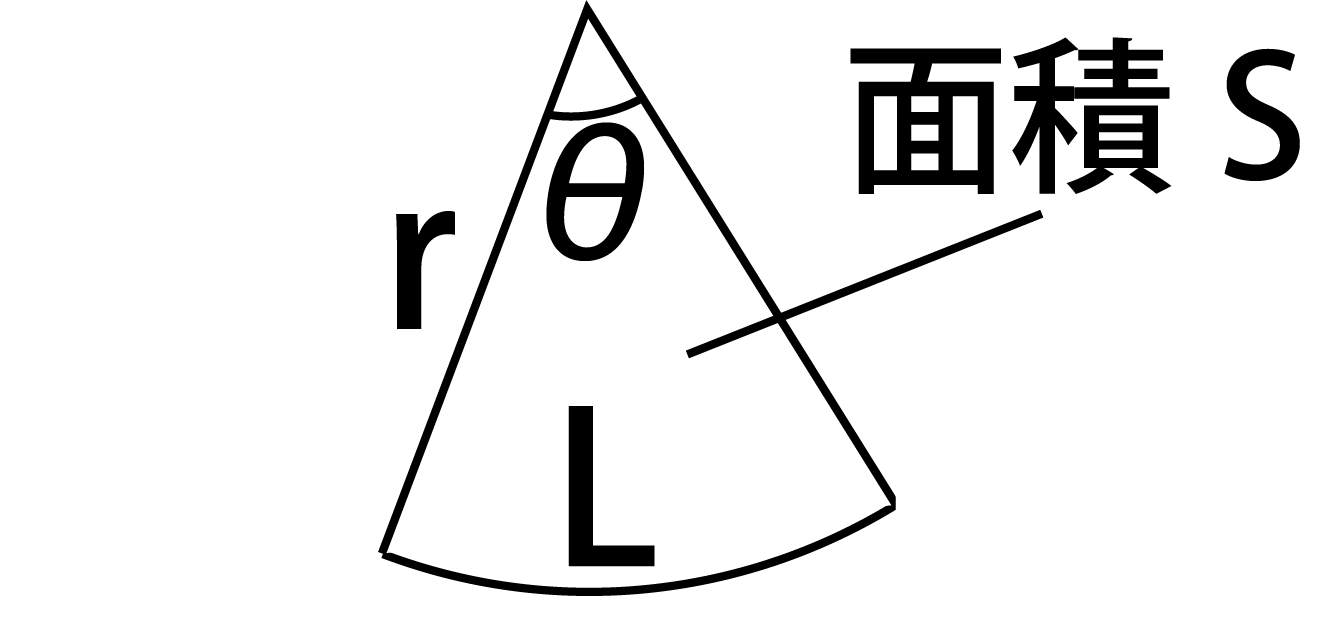



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




ボード 復習 のピン




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
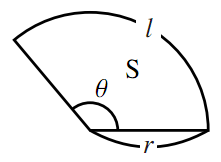



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
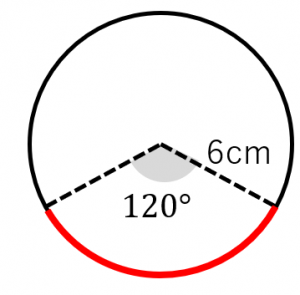



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




円の周りの長さを計算しよう 家庭学習レシピ




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張
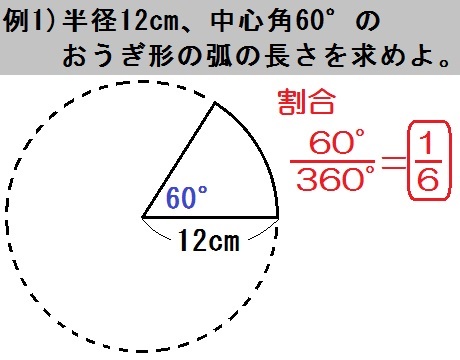



中学数学 平面図形 のコツ 円とおうぎ形




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




おうぎ形の弧の長さの公式 算数の公式




標準 おうぎ形と正方形の面積 なかけんの数学ノート




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー
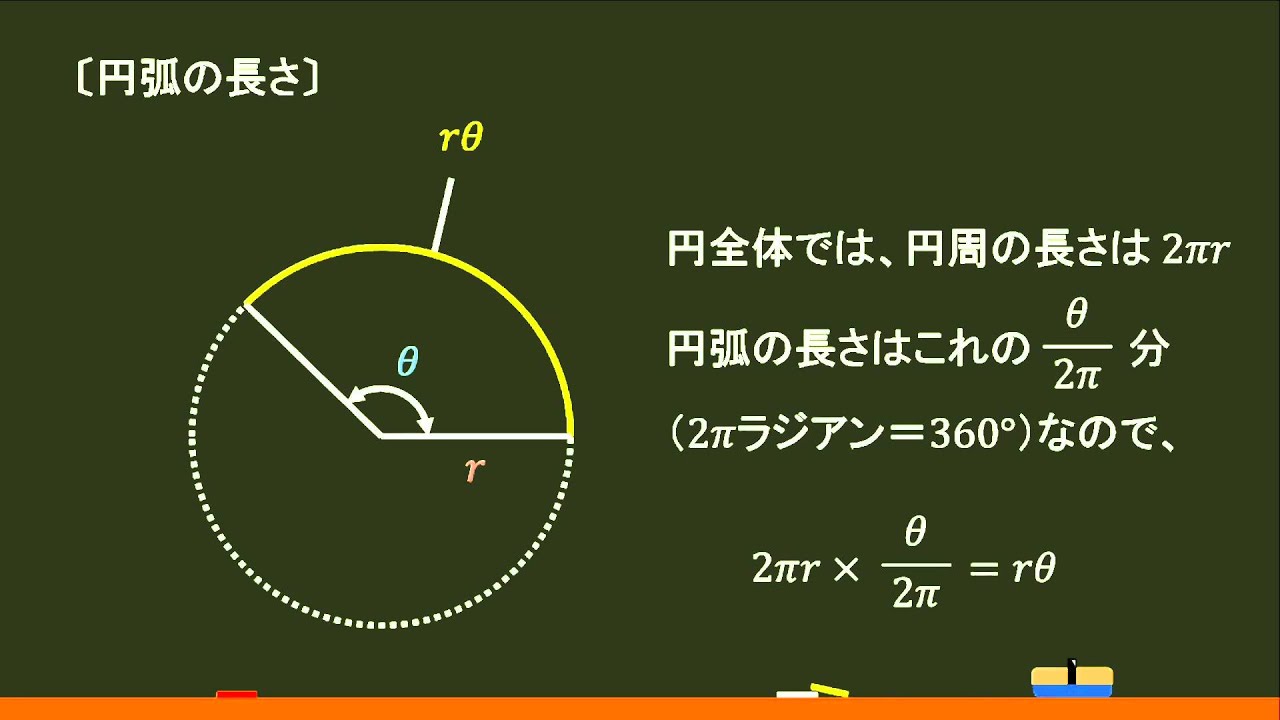



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の中心角の求め方を教えて下さい Clear




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
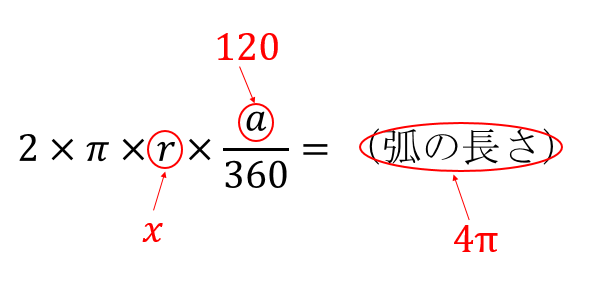



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
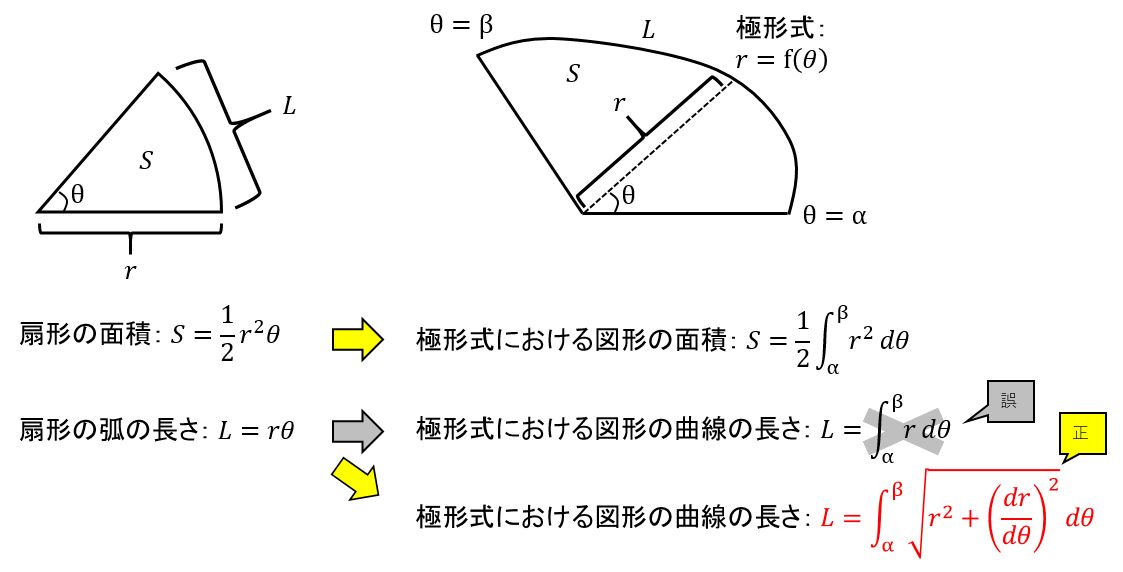



Lさんのツイート 今ミスしたことをまとめました 極形式について 面積は扇形から公式が作れるのですが 曲線の長さは扇形から作れません D 作れない理由は Rとr 2における近似レベルの違いな気がしますが 詳細は調べてません 数学 数検 高校
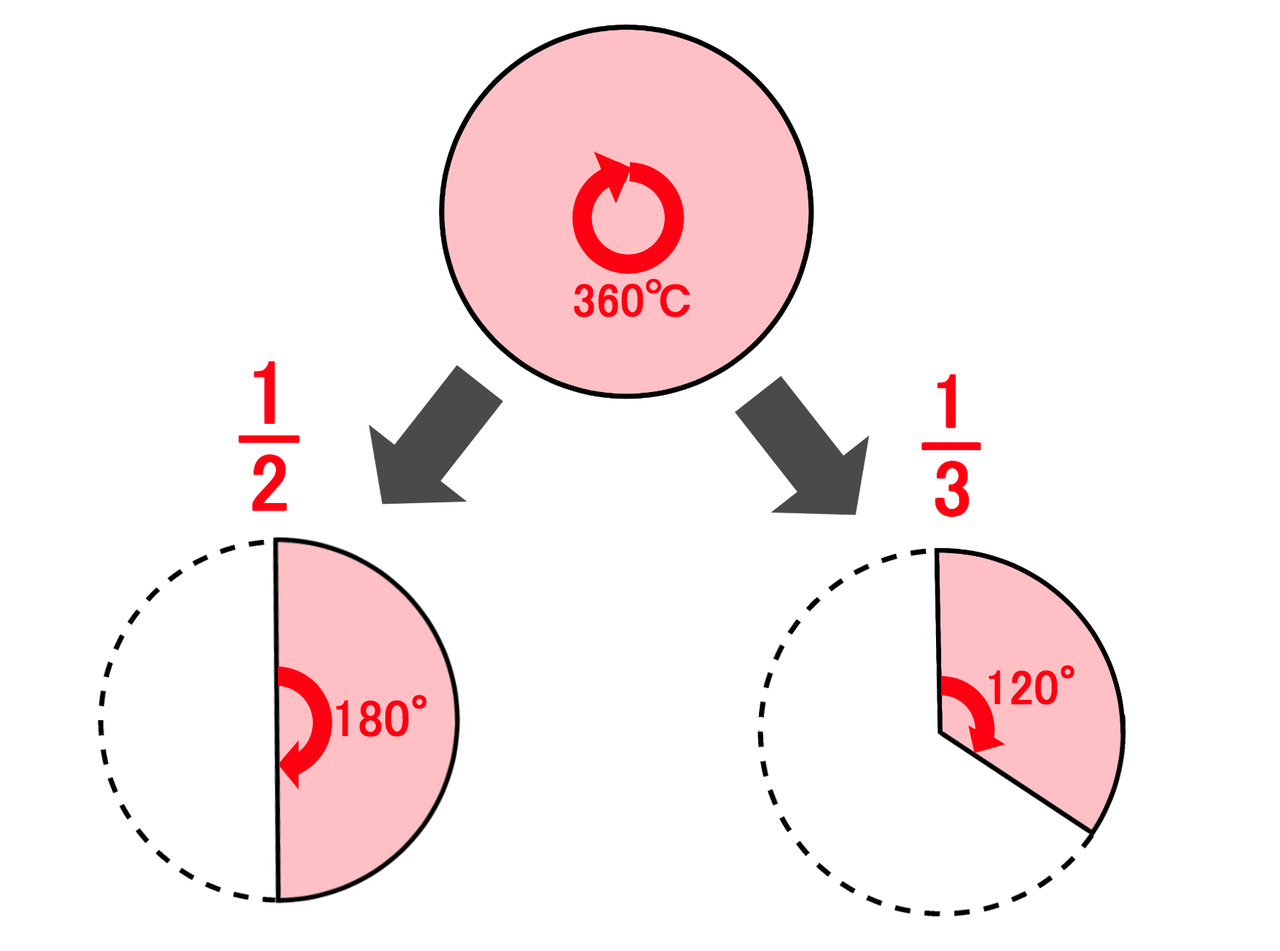



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく



受験数学かずスクール 扇形の弧の長さと面積




扇形の面積 弧の長さ 計算機 かんたん計算機




扇形の弧の長さと面積 計算ドリル 問題集 数学fun




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学




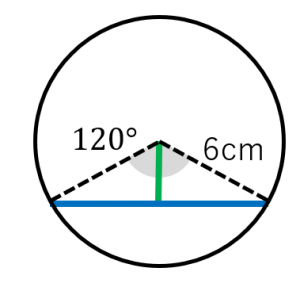
O Xrhsths 数学 Ii Sto Twitter 第1節 三角関数 角の拡張 D 弧度法と扇形 画像右 例題 半径4 中心角pの扇形の 弧の長さℓと面積sを求めよ
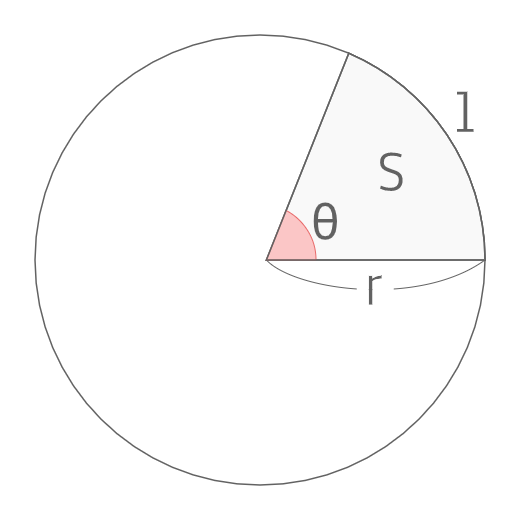



高校数学 扇形の弧の長さと面積 の公式とその証明 Enggy




扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube
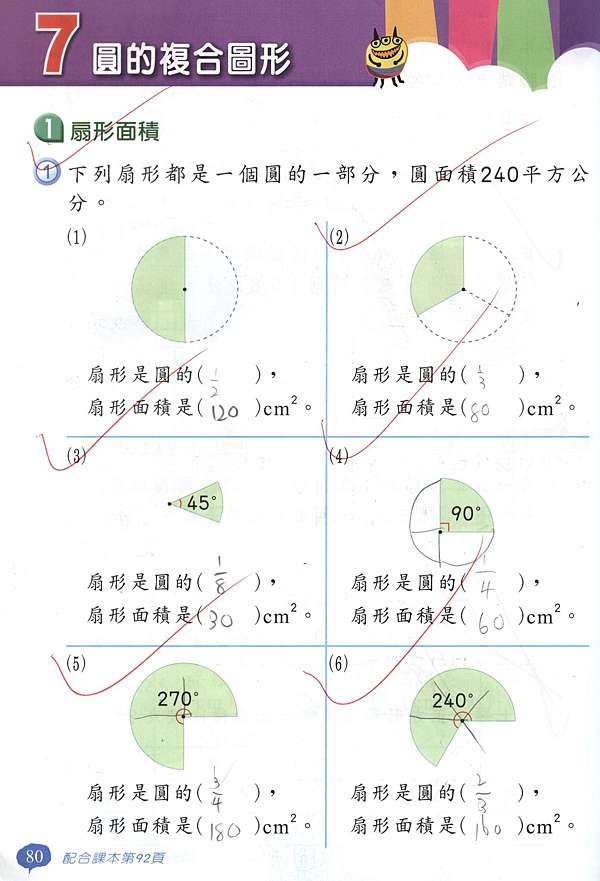



扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




弧長 Arc Length Japaneseclass Jp




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋



コメント
コメントを投稿